本文共 2509 字,大约阅读时间需要 8 分钟。
目录 :
目录
讨论比特币的加密算法,椭圆曲线始终是绕不开的坑。以下笔记是观看比特币加密教程总结而成,图片来源于网络。
ECDSA算法
椭圆曲线乘法(又称为ECDSA)是密码学重要的非对称加密算法,同时在比特币系统中,私钥的生成使用的也是ECDSA算法。比特币使用了secp256k1标准定义的一条特殊的椭圆曲线和一系列数学常数
椭圆曲线
认识椭圆曲线
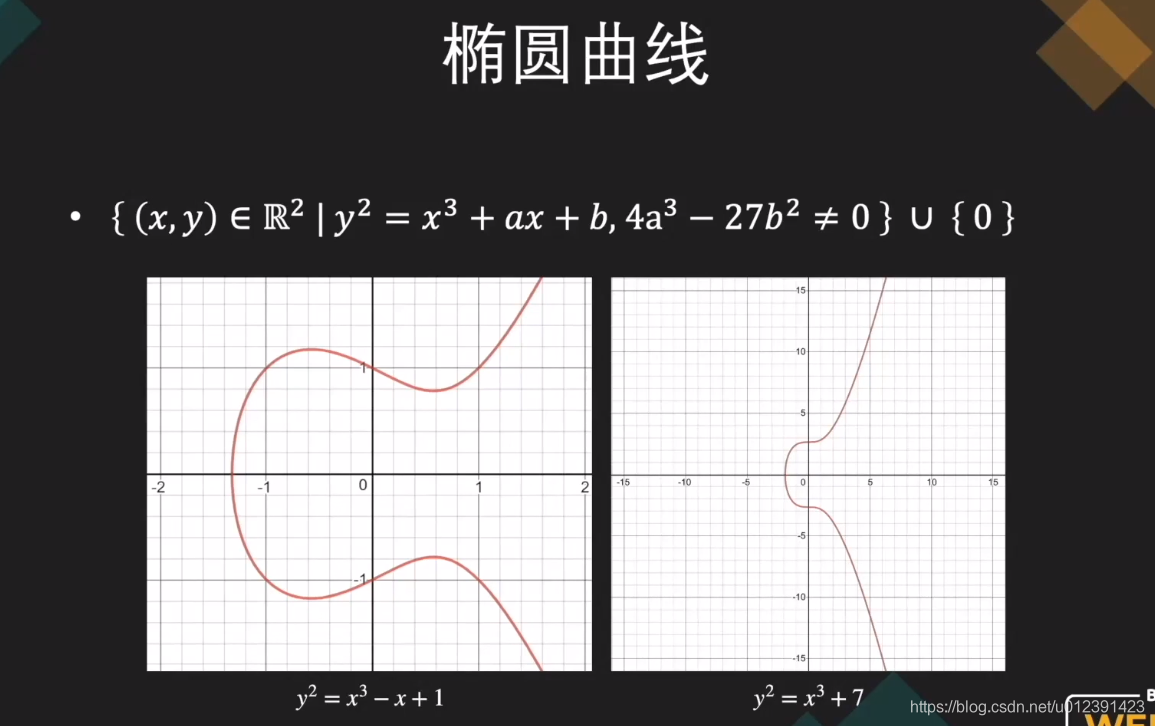
椭圆曲线不是一个椭圆,而是满足上图方程的x、y点的连续集合。解读一下该方程
1、x、y 是两个实数
2、a、b是两个常量,并且满足 4a² - 27b³ ≠ 0
3、满足 y² = x³ + ax + b
4、包含无穷远点 ,我们定义无穷远点即是0
注意:
1、椭圆曲线不是一条线,而是一群,不同的a、b取值,呈现不同的曲线,如上图。比特币使用的曲线是secp256k1
2、曲线上任意两点P、Q连接成直线,一定且只能与该曲线相交于第三点 -R
3、曲线不一定关于x轴对称
椭圆曲线上点的加法

注意:我们这里讨论的加法是几何学的加法,不要与代数学加法混淆。
简单来说 一条直线与椭圆曲线相交于3个点,分别为 P、Q、-R , 则有 P + Q = -R 推导出 P + Q + R= 0;
这里我们将分情况讨论:
1、假设 Q = 0 即 Q在无穷远处 ,是无穷远点 , 则 P + Q = P + 0 = P
2、假设 两点关于X轴对称,如上图 R 、-R , 则 R + (-R) = 0 ; 怎么理解? R 与 -R 连接成直线 , 与Y轴平行,与椭圆曲线相交于无穷远点 , 也就是 0
3、假设 P != Q , PQ直线与椭圆曲线相交于 -R 点 , 则 P + Q = R ; 怎么理解? P、Q、-R 三点的直线,与椭圆曲线相交于无穷远 , 即 P + Q + (-R) = 0 => P + Q = R
4、假设 P = Q ,过P点的切线 , 与椭圆曲线相交于 -R点 , 则 P + Q = -R => 2P = -R
椭圆曲线上点的数乘
现在,假设曲线上的点G , 我们要求 曲线上的点 N = 8 * G , 我们可以按照加法来做 , 即 N = 8 * G = G + G + G + G + G + G + G + G ; 但是有个问题 , 如果不是求8G , 而是8000G 、 80000G呢 , 这个计算量是非常大的 , 所以我们可以采用 “倍乘法” , 如下图:

倍乘法的流程如下:
1、 过 G点做切线 , 与椭圆曲线相交的点即为 -2G , -2G = G + G
2、 -2G点 上下翻转 , 得到 2G交点
3、过 2G点做切线 , 可以计算获得 -4G = -2G + -2G
4、-4G点 上下翻转 , 得到 4G交点
5、依次类推......
有限域的椭圆曲线
椭圆曲线 , 是连续的曲线 , 其上所有的点都是实数(有小数) , 但计算机的精度误差,保留小数是有限制的,明文经过加密解密后会出现偏差,得不到原来的明文。 因此 , 我们需要一群离散的整数点 ,来满足加密的要求 。 这便是我们下面要将的有限域椭圆曲线。
如何得到有限域曲线呢 , 我们需要先了解一下几个概念:模运算、同余、有限域
-
模运算 (mod)
简单来讲就是求商取余,比如:
5 除以 3 等于 1 ,余数 =2 , 我们可以表示为 5 mod 3 = 2 , 这就是模运算。
我们整理一个通用的公示 a mod b = r ,模运算有以下特性 :
(a + b) mod c = { (a mod c) + (b mod c)} mod c
(a * b) mod c = { (a mod c) * (b mod c)} mod c
(a^b ) mod c = ( a mod c )^b mod c
-
同余
a、b两个数 除以 c , 所得余数相同 即是同余 , 我们可以表示为: a mod c = b mod c 或者 a b ( mod c)
假如 k ∈ Z ( k属于整数 ), a b (mod c) <==> ka
kb (mod c)
比如 k =3 , 2 6 (mod 4) , name 3*2
3 * 6 (mod 4)
-
有限域
顾名思义就是有限的元素集合 , 比如 Z mod 7 = {1,2,3,4,5,6} , 这就是一个有限域
-
有限域椭圆曲线
根据椭圆曲线公式 , y² = x³ + ax + b , 令 a = -7 , b = 10 ,
确定后的椭圆曲线公式 , y² = x³ - 7x + 10
那么, 我们如何设定有限域 ? 如何只取整数的点呢 ? 如何使曲线离散呢 ? 我们只需要这样
1、Fp中有p(p为质数)个元素0,1,2,…, p-2,p-1
2、x 、y ∈ Fp
3、y² = x³ - 7x + 10 (mod p)
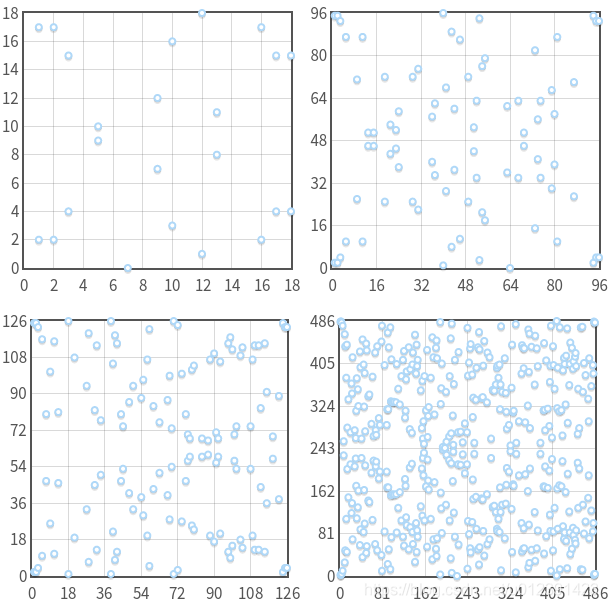
当p 取不同值时 p = 19,97,127,487, 离散后的图如下,可见p的值越大 , 离散的点越多
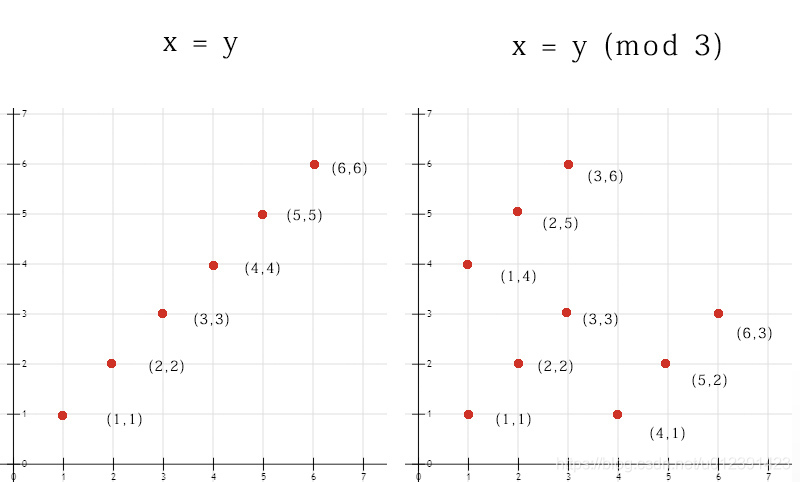
是不是不太明白 , 为啥 mod p 就离散了 , 不连续了呢 ? 我们换一个简单的公式来解释一下 , 假设 x、y ∈ {1,2,3,4,5,6} , p =3
-
有限域椭圆曲线上的直线
有限域上满足方程式的 (x,y)点 , 全部离散了 , 已经无法连成一条椭圆曲线了,也就无法用一条直线连接曲线上的3个点了,那么我们如何做加法? 如何做数乘呢?
显然,我们需要对加法的定义稍作更改,以使其在 Fp。对于实数,我们说三个对齐点的总和为零(P+Q+R=0)。我们可以保留这个定义,但是在Fp中将三个点对齐是什么意思?
我们可以说,如果有一条直线将所有三个点连接在一起,那么这三个点是对齐的。但是,Fp 与 R是不同的。Fp 是点集 (x,ÿ) 满足方程式 ax+bÿ+c≡0(mod p) (这是标准线式,加上“(mod p)”)。

-
有限域椭圆曲线的代数加法
未完待续。。。。
Secp256k1
secp256k1曲线上点运算性质
椭圆曲线为什么不可逆
转载地址:http://ukzp.baihongyu.com/